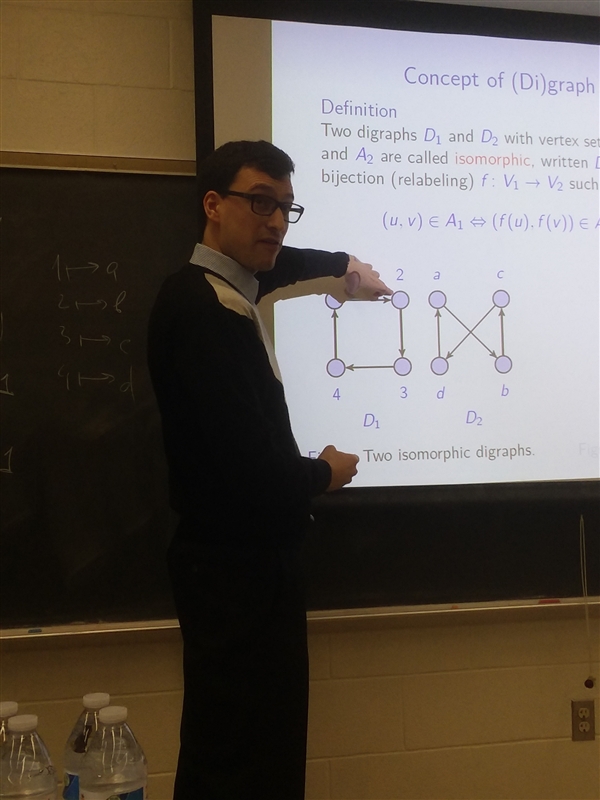Mathematics Colloquia
-
Dr. Grant Fickes (Department of Defense)
Friday, November 17, 2023 at 3:00 p.m. in Lytle 214
- Abstract:
We split our time in two. In the first half, we discuss what it looks like to
be a working mathematician and how you might prepare yourself for a career in
mathematics. In the second half, we study nullvectors of trees. We define the
zero locus of a nullvector to be the set of coordinates which correspond to zeros
of the vector and the zero locus of a graph to be the intersection of the zero locus
over all nullvectors. We present ways to determine the zero locus of a tree and
properties of a tree's zero locus. Finally, we motivate the study by considering the
analogue of the question for linear hypertrees.
- Abstract:
-
Mr. Isaac Reiter (Lehigh University): "Graduate School: What to Expect, How to Prepare, and How to Succeed"
Tuesday, November 7, 2023 at 4:30 p.m. in Boehm 261
-
Dr. Gene Fiorini (DIMACS-Rutgers University): "On Some Properties of Pebble Assignment Graphs"
Tuesday, November 8, 2022 at 3:00 p.m. in Lytle 214
- Abstract:
A pebble assignment graph (SG) on a finite simple graph G is a distribution of a finite number of pebbles on the vertices of G. A standard pebbling move consists of removing two pebbles from a vertex v of G while adding one pebble to a vertex adjacent to v.
In this talk, we introduce the new notion of a pebble assignment graph. Formally, this is a Hasse diagram [SG] whose nodes correspond to all assignments that can be reached from (SG) by applying a sequence of pebbling moves. Edges of [SG] adjoin any two assignments where one can be reached from the other via a single pebbling move (i.e. from "parent" to "child"). We investigate properties of this new class of graphs, and explore variations on the original construction.
- Abstract:
-
Mr. Michael Pol (Prosoft Clinical): "Transitioning into a Career as a Statistician Working in Clinical Research"
Thursday, November 3, 2022 at 11:00 a.m. in Boehm 261
- Abstract:
In a world where analytics are more in demand than ever, a mathematics degree can land you in a variety of interesting fields. We will discuss potential paths towards a career coming out of undergraduate studies, as well as the importance of familiarizing yourself with statistical programming languages. We will briefly touch upon my experience working in Sales/Marketing analytics for pharmaceutical companies before moving on to a more in-depth discussion of working for a Contract Research Organization (CRO) in support of clinical trials. This discussion will include an application of simulating random variables to generate type 1 error as well as the process of publishing a scientific paper. We will then discuss the various day to day tasks of a statistician working for a CRO from helping with study planning to generating CDSIC data to producing tables that summarize the data. This will include the role of the client and the FDA in these tasks.
- Abstract:
-
Ms. Michelle Cramer (Andesa Services, Inc.): "Your Journey to Becoming an Actuary"
Thursday, November 18, 2021 at 11:00 a.m. in Boehm 261
- Abstract:
Actuarial science has been a growing field for the past decade, and it is projected to continue to grow over the next decade. This is one of the most successful and engaging career choices for math and computer science majors. Michelle Cramer will tell us about her journey to becoming an actuary and about important information you will need to be a successful actuary.
- Abstract:
-
Mr. Grant Fickes (University of South Carolina): "Characteristic Polynomials and Spectra of Rank k Hypergraphs"
Friday, February 14 at 3:00 p.m. in Lytle 214
- Abstract:
Spectral graph theory studies properties of a graph in relation to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph. The set of eigenvalues of the adjacency matrix is called the spectrum of a graph. In this talk we explore a background in spectral graph theory and the work that has been done to extend results to hypergraphs with rank k. We discuss challenges of spectral hypergraph theory, known results, and current research interests.
- Abstract:
-
Mrs. Lorinda Leshock (KU Dept. of Mathematics): "Pappus Configurations in Finite Hall Affine Planes"
Tuesday, November 12 at 3:00 p.m. in Lytle 214
- Abstract:
In the classical projective planes, both the Desargues theorem and Pappus theorem hold. According to a result of Ostrom, the Desargues configuration can also be found in every finite projective plane on at least twenty-one points, classical or not. In fact, it was shown that the number of Desargues configurations in every finite plane is actually quite large. The existence of a Pappus configuration in every non-classical finite affine or projective plane is unknown. We study whether the Pappus configuration is present in such planes.
In particular, we endeavor to prove that in finite Hall affine planes on more than eighty-one points, the following strong version for the exitence of the Pappus configuration holds: For every pair of lines l_1, l_2, every triple of points on l_1 and every point on l_2, two more points can be found on l_2 that define a Pappus configuration. Hall planes are not Pappian, yet the proof of this statement will imply that the number of Pappus configurations in Hall planes is actually quite large (this is a joint work with Felix Lazebnik).
- Abstract:
-
Dr. Alex Kodess (SUNY Farmingdale): "Algebraically Defined Directed Graphs"
Friday, March 22 at 3:00 p.m. in Lytle 214
- Abstract:
Given a finite field F_q of size q, consider a directed graph (digraph) with vertex set F_q x F_q, in which there is an arc from a vertex (a,b) to a vertex (c,d) if b+d = f(a,c) for some f in F_q[X,Y], a bivariate polynomial. Motivated by an unexpected result concerning the number of roots of certain polynomials over F_q, we look at the isomorphism problem for these digraphs. Other problems such as the diameter problem will be considered, too.
We will also look at some of the generalizations of this construction and at a number of open questions related to them.
All relevant terms will be defined and no prior knowledge of graph theory or finite fields is required.
- Abstract:
-
Dr. Yun Lu (KU Dept. of Mathematics): Chambliss Faculty Research Lecture -- "Optimization by Metaheuristics"
Monday, November 19 at 4:30 p.m. in MSU 183
- Abstract:
Metaheuristics are high-level problem-independent algorithmic frameworks that provide a set of guidelines or strategies to develop heuristic optimization algorithms. They are generally recognized as efficient approaches to solve complex problems in industry and services, in areas ranging from finance to production management and engineering. Lu will provide an overview of some main metaheuristics and their principles, as well as give examples of how certain metaheuristics are used to solve combinatorial optimization problems.
- Abstract:
-
Dr. Sarah Tindall (KU Dept. of Geology): "Math, geology, and you. Yes...YOU!"
Thursday, November 15 at 11:00 a.m. in Lytle Hall 228
- Abstract:
Dr. Tindall will explain some of the ways math is used in geology, as well as an exciting summer research opportunity YOU might be interested in that explores this connection.
- Abstract:
-
Dr. Megan Cream (Mathematics Dept., Cedar Crest College): "Extensions of Pancyclicity"
Thursday, November 1, 2018, at 3:00 p.m. in Lytle Hall 218
- Abstract:
This talk will serve both as an introduction to the exciting field of graph theory, as well as an exploration of a recent research topic in the field. In particular, we will discuss the properties of cycles in graphs. A graph G on n vertices is called pancyclic if it contains a cycle of every possible length, from three to the order of the graph, n. Further, a graph is vertex pancyclic (or edge pancyclic) if every vertex (edge) is contained on a cycle of every possible length, from three to n. Recently, these cycle properties and a few variations of these properties have been extended to chorded cycles in graphs. We will discuss results on minimum degree and degree-sum conditions necessary to imply these pancyclicity properties in graphs.
- Abstract:
-
Mr. Ben Orlin: "The Unlikely Friendship of Math and Science"
Mr. Ben Orlin, the author of "Math with Bad Drawings: Illuminating the Ideas That Shape Our Reality" as well as the blog https://mathwithbaddrawings.com/
Monday, October 29, 2018 at 7:00 p.m. in Boehm Hall 261
- Abstract:
Math is supposed to be useful. And yet mathematicians are always chasing imaginary visions, abstractions divorced from reality. Could that possibly prove useful to science? Actually, yes. In a big way.
This talk is intended for undergraduate students, high school students, their families, and members of the community!
- Abstract:
-
Dr. Myung Soon Song (KU Dept. of Mathematics): "A Numerical Likelihood-Based Approach to Combining Information"
Thursday, October 11, 2018, at 11:00 a.m. in Lytle Hall 228
- Abstract:
Numerical approximations are important research areas for dealing with complicated functional forms. Techniques for developing accurate and efficient calculation of combined likelihood functions in the meta-analysis are studied.
A multivariate numerical integration method for developing a better approximation of the likelihood for correlation matrices is studied. Analyses for inter-correlations among Cognitive Anxiety, Somatic Anxiety and Self Confidence from Competitive State Anxiety Inventory (CSAI-2) are explored.
Evaluation and Visualization of the likelihood and the MLE is conducted. Comparison with two conventional methods (joint asymptotic weighted average method & marginal asymptotic weighted average method) is shown.
- Abstract:
-
Dr. Christopher Krizan (KU Dept. of Mathematics): "Szlam Numbers and their Relationship to Chromatic Numbers"
Tuesday, September 24, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
If we color every point in the real plane either red or blue such that no two points colored blue are unit distance apart in the Euclidean sense, then one can pose the following problem. Find a set of points in the plane that has no translation in which all points are red (an all-red set).
As a consequence to a result by Johnson and Szlam, the cardinality of such a set is an upper bound of the chromatic number of the plane, that is, the minimum number of colors needed to color every point in the real plane such that no two points of unit distance are monochromatic; again, distance is Euclidean.
We explore the relationship between these two problems using graph theory and in particular we explore both problems with different notions of distance that are translation invariant.
- Abstract:
-
Dr. Brooks Emerick (KU Dept. of Mathematics): "Exploring Pattern Formation and Turing Instability in Reaction-diffusion Systems"
Thursday, March 29, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
In 1952, Alan Turing, considered by many as the father of modern computer science, published a set of equations that tried to explain the patterns we see in nature.
In general, these equations are a subset of reaction-diffusion equations, which track the space-time evolution of a pair of interacting chemical concentrations. Today, the idea of Turing patterns can involve not just chemicals, but large, complex systems in which each unit of a concentration or population is distributed like molecules of a pigment. It is generally accepted (and confirmed experimentally) that markings on animals are produced by Turing systems of pigments, but the origin of what appear to be Turing patterns in more complex settings like limb or organ development is still debated.
In this talk, we will discuss the wide range of applications associated to pattern formation and the elements that make up interesting reaction-diffusion systems that yield Turing instability. In addition, we will explore the different patterns that are possible through various simulations.
- Abstract:
-
Dr. Myung Soon Song (State University of New York at Cortland): "Synthesizing Correlations by Numerical Likelihood Approach with Applications"
Thursday, March 22, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
A likelihood-based approach with numerical approximation for synthesizing correlation coefficients is studied. The maximum likelihood estimator (MLE) and the likelihood interval are used for inference.
This approach can be easily extended to the realm of meta-analysis involving sample correlations from different, independent studies by use of a combined likelihood function. The sample correlations between vitamin C intake and serum level of vitamin C from many studies are used to illustrate application of this approach.
A simulation is conducted for comparison with conventional methods.
- Abstract:
-
Ms. MengMeng Guo (Mathematics Dept., Texas Tech University): "Statistical Shape Analysis of Curves"
Tuesday, February 20, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
We develop a multivariate regression model when response variable is on nonlinear manifolds, rather than on Euclidean space. This non-linear constraint makes the problem challenging and needs to be studied carefully. By performing principal component analysis on tangent space of manifolds, we use the principal directions as our response variables instead. Then, the ordinary regression tools are utilized.
We apply the framework to the problem of ozone depletion and its influencing factors. Particularly, these ozone hole contours are considered as response observations on manifold, where the manifold is equipped with a parametrization-invariant metric. Experimental results have shown that we can not only find the most significant factors, but also predict ozone hole contours by the constructed model.
- Abstract:
-
Mr. Mingwei Sun (Mathematics Dept., University of Alabama): "Regression Models with a Universal Penalized Function"
Thursday, February 15, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
Variable selection is an important topic in linear regression analysis and attracts considerable research in this era of big data. It is fundamental to high-dimensional statistical modeling, including non-parametric regression. Some classic techniques include stepwise deletion and subset selection. However, these procedures ignore stochastic errors inherited in the stages of variable selections and the resulting subset suffers from lack of stability and low prediction accuracy.
Penalized least squares provide new approaches to the variable selection problems. The LASSO which imposes an L1-penalty on the regression coefficients and the elastic net which combines an L1 and an L2 penalties are popular members of the penalized least squares.
In this research, we develop penalized regressions of universal penalty function and prove that the LASSO and elastic net are special cases of our function. The structure and properties of universal penalty are studied and the corresponding algorithms are developed. We apply our model to a real U.S. economic and financial data example. Simulation studies and real-data applications support the advantageous performance of the proposed methods.
- Abstract:
-
Mr. Yeil Kwon (Dept. of Statistical Sciences, Temple University): "Nonparametric Estimation of Simultaneous-Selected Variances (NESV)
Thursday, February 8, 2018 at 11:00 a.m. in Lytle Hall 228
- Abstract:
The shrinkage estimation, one of the empirical Bayesian approaches, has proven to be very useful when facing with a large number of mean parameters to be estimated. In the modern application, it is not uncommon to estimate a large number of variances simultaneously. We construct a non-parametric estimation of simultaneous/selected variances (NESV). Namely, we take the f-modeling approach and assume an arbitrary prior on the variances.
Under an invariant loss function, the resultant Bayesian decision estimator relies on the marginal cumulative distribution function only, which can be reliably estimated using the empirical distribution function. We applied the proposed NESV to construct the confidence intervals for the mean parameters post the selection. It is shown that the intervals based on the NESV are shortest among all the intervals which guarantee a desired coverage probability.
Through two real data analysis, we have further shown that the NESV based intervals lead to the smallest number of discordant parameters, a favorable property when facing with the current “replication crisis.”
- Abstract:
-
Dr. Mark Wolfmeyer (KU Dept. of Secondary Education): "Open Questions in Mathematics Education (Parts I and II)"
- Thursday, November 9, 2017 at 11:00 a.m. in Lytle Hall 228
- Thursday, October 12, 2017 at 11:00 a.m. in Lytle Hall 228
- Abstract:
In this interactive session, participants will discuss and learn about some more of the more often debated policy topics in K-12 teaching and learning of mathematics.
For each topic, Dr. Wolfmeyer will open with a prompt for discussion, review the policy and research debates related to the question, and set time for small group and whole-group discussion. Potential topics, listed here as "open questions'' include:
- Should K-12 mathematics learning emphasize conceptual understanding of mathematics? - Should all students be required to take mathematics? Should the US have a national
mathematics curriculum?
- What are the more critical aspects to preparing future K-12 mathematics teachers?
- Does mathematics teaching and learning have anything to do with race, social class, and
gender?
- What is the purpose of teaching mathematics?
- Who should make decisions about mathematics education policy?
-
Dr. Karen McCready (King's College): "Connecting the Dots & Coloring Paths: Adventures in Graph Theory"
Thursday, April 13, 2017 at 11:00 a.m. in Lytle Hall 214
- Abstract:
In this talk we will look at some basic properties of graphs as well as some classical problems that arise in the study of graph theory. We will also consider a modification of the diameter of a graph for edge-colored graphs, called the proper diameter, which is a function of both the graph and its coloring. This will lead us to explore the relationship between the diameter and proper diameter of certain graph classes.
- Abstract:
-
Ms. Katelynn Kochalski (University of Virginia): "Fluid Limit for a Batched Processor Sharing Queue"
Tuesday, February 14, 2017 at 3:00 p.m. in Lytle Hall 214
- Abstract:
In queueing theory we refer to the items in the queue as jobs and the rule that dictates how jobs are processed as the service policy. A common service policy is First-In-First-Out (FIFO). In FIFO, the job that has been waiting in line the longest is served next. This is the service policy that is used in line at the grocery store or bank. We study a sequence of queues operating under a service policy where the system creates batches and works on multiple jobs at a time. Motivated by the law of large numbers from classical probability, we find a fluid limit for the queues. This limiting result provides a simple description for a complicated system. We can then use this simpler limiting object to approximate what happens in the system. In particular, we show the model is completely described by its initial state and each batch will start in a predictable, periodic way.
- Abstract:
-
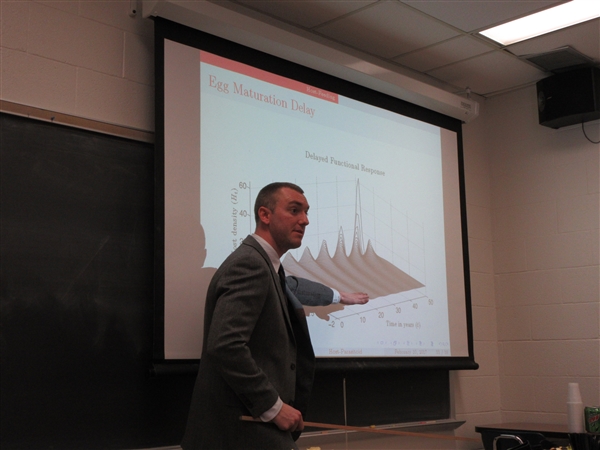
Dr. Brooks Emerick (Trinity College): "Attack of the Tiny Titans"
Friday, February 10 at 3:00 p.m. in Lytle Hall 214
- Abstract:
This talk will discuss the mathematical modeling approach to describe the interactions of a host and a parasitioid a.k.a. tiny titan. A parasitoid is an organism that spends a portion of its life attached to or within a single host organism. Unlike a parasite, a parasitoid will eventually kill or consume the host. Discrete-time models are the traditional approach for capturing population dynamics of a host-parasitoid system. Recent work has introduced a semi-discrete framework for obtaining model update functions that connect population levels from year-to-year. In particular, this framework uses differential equations to describe the host-parasitoid interaction during the time of year when they come in contact allowing specific behaviors to be mechanistically incorporated. We'll introduce the traditional methods used and present results from models that include behaviors such as host-feeding, parasitoid migration, and variation of risk.
- Abstract:
-
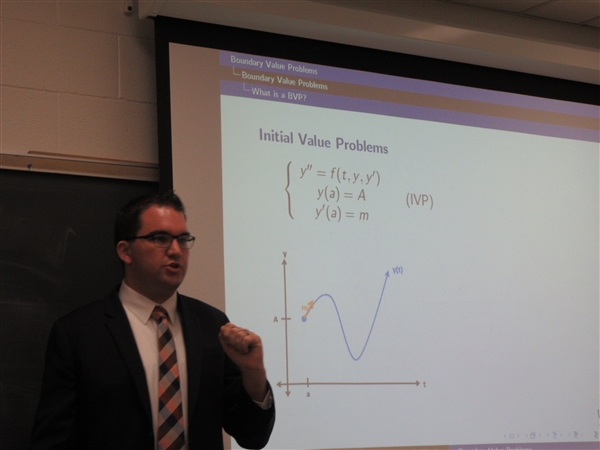
Mr. Quinn Morris (UNC-Greensboro): "From Theory to Practice: Boundary Value Problems and Prokelisia marginata"
Tuesday, February 7, 2017 at 3:00 p.m. in Lytle Hall 214
- Abstract:
In a first course in ordinary differential equations, one often treats initial value problems of the form u'' + f(u) = 0, u(a)=u_0, u'(a)=u_1, and is able to show existence & uniqueness of such solutions when $f$ is ``nice." In this talk, we will instead consider boundary value problems of the form u'' + f(u) = 0, u(a)=u_0, u(b)=u_1, and observe that even for very "nice" functions f, we can get very exotic behavior. At the end of the talk, we will examine a boundary value problem from population dynamics which is of recent interest.
- Abstract:
-
Ms. Lizzy Huang (Duke University): "Harmonic maps with repulsive potentials"
Tuesday, January 31, 2017 at 3:00 p.m. in Lytle Hall 214
- Abstract:
Many questions in topology and physics can be expressed in terms of finding a function $f$ between a curved space $M$ (the domain) and another curved space $N$ (the target) which minimizes a natural energy functional: $\int_M |df|^2 dx$. Functions that minimize this energy are called harmonic maps. One method to obtain a harmonic map is to consider a family of maps $f_t$ which follow a path of `steepest descent.' In this talk, I will discuss a modification of this approach in which an unbounded potential energy is added to the total energy. Then I will discuss the behavior and singularities of the limiting maps in cases of special significance to topology. I will only assume knowledge of multivariable calculus for this talk.
- Abstract:
-
Mr. Nathaniel Benjamin (KU '17 - Math and Secondary Education Math Major): "The Research Experience: Selected Topics in Graph Theory"
Thursday, September 22, 2016 at 3:30 p.m. in Lytle Hall 228
- Abstract:
This talk will initially address Research Experiences for Undergraduates (REUs) in a general sense by providing anecdotal descriptions and explanations, elaborating on some semantics and the benefits of such. The primary focus of the talk, however, will be on a component of the product of the Summer 2016 OEIS REU hosted by Muhlenberg College.
Graph Theory, being one of but seven projects that constituted the summer research experience, was a major topic investigated by numerous participants of the program. A large portion of the results of this research will be presented in the talk, specifically on the work completed regarding edge-distinguishing chromatic numbers and the Catalan triangle. The former topic refers to an unusual method of vertex coloring on a given graph to ensure distinct edge colors defined as an unordered pair of colors. The latter topic investigates the presence of unique, or rather non-unique, integers on an interesting number triangle constructed fundamentally from the Catalan numbers.
- Abstract:
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016

Colloquium Series
2015-2016









-
Dr. Michelle Savescu (KU Dept. of Mathematics): "Soliton Solutions of the Nonlinear Schrödinger Equation"
Tuesday, March 29, 2016 at 3:00 p.m. in Lytle Hall 218
- Abstract:
The presentation starts with a brief history of solitons followed by an introduction to optical solitons and related concepts. The dynamics of the propagation of solitons through optical fibers is governed by the Nonlinear Schrödinger Equation (NLSE).
Several methods have been applied to the NLSE in order to obtain analytical soliton solutions. The methods that will be presented here are the traveling wave hypothesis, the ansatz method, the semi-inverse variational principle, the tanh method, the G′/G expansion method and the Adomian decomposition method.
Research results using some of these methods will be presented for physical models such as nano optical fibers and birefringent fibers. Bright, dark and singular soliton solutions were obtained for nonlinearity laws such as the Kerr law, the parabolic law and the polynomial law of nonlinearity.
- Abstract:
-
Dr. Mark Wolfmeyer (KU Dept. of Secondary Education): "Who's Who in the Politics of Math Education"
Thursday, March 24, 2016 at 11:00 a.m. in Boehm Hall 260
- Abstract:
The effort to standardize a US national mathematics curriculum culminated in 2010 when over 40 states adopted the Common Core State Standards for Mathematics. How did this come to be? Who was involved and what did they set as the primary issues in mathematics education? This talk aims to provide a landscape of mathematics education policy in the United States and draws on Dr. Wolfmeyer's research contained in Math Education for America? (Routledge, 2014).
In an interactive presentation he will offer examples of the people and organizations involved in mathematics policy, shedding insight into the debates that exist and priorities now established. Come, mathematicians and educators, and find out where you stand on today's most pertinent issues in K-12 mathematics teaching and learning!
- Abstract:
-
Dr. Tuan Nguyen (University of Southern California): "An Evaluation of the Functional Assessment Questionnaire Using a Graded Response Model"
Tuesday, March 22, 2016 at 3:00 p.m. in Lytle Hall 228
- Abstract:
Alzheimer's disease (AD) is widely believed to progress over many years before any clinical symptom appears; hence, an effective treatment should be started as early as possible, especially in the preclinical stage of AD. One of the challenges to achieve this end is to find endpoints that have good sensitivity to the longitudinal decline of global functional performance.
The currently available measurements are typically obtained by assessing the patient performance on a Likert scale and summing up the resulting sub-scores to yield overall performance. An alternative approach, explored in this work, is to compute the measurement under item response theory (IRT).
Using data on the Functional Assessment Questionnaire from the Alzheimer's Disease Neuroimaging Initiative (ADNI) study, we found that IRT-based scoring increased the sensitivity to change in functional ability and improved the statistical power in future clinical trials.
- Abstract:
-
Dr. Christopher Goodrich (Creighton Preparatory School): "An Analysis of Non-local Elements in Differential Equations and Fractional Calculus"
Monday, February 29, 2016 at 3:00 p.m. in Lytle Hall 214
- Abstract:
In this talk we will discuss the effect of non-local elements in the discrete and continuous calculus. More specifically, we will investigate two different manifestations of non-local elements:
1. the analysis of boundary value problems with nonlocal boundary conditions; and
2. the nonlocal structure of the discrete fractional difference.
Finally, since we will begin by discussing the fundamentals of both the difference calculus and boundary value problems, no previous knowledge of each is assumed. A working knowledge of single-variable calculus and ordinary differential equations should be sufficient to understand a majority of the talk.
- Abstract:
-
Dr. Sara W. Lapan (Northwestern University): "A Snapshot of Complex Dynamics"
Tuesday, February 23, 2016 at 3:00 p.m. in Lytle Hall 228
- Abstract:
Complex dynamics is a fascinating area of mathematics that lies at the intersection of complex analysis and dynamical systems. In pop-culture, complex dynamics is known for its beautiful fractals, like the Mandelbrot set and Julia sets. This talk will be a gentle introduction to complex dynamics and, along the way, we will see and explore many beautiful fractals.
More specifically, we will focus on polynomials P(z) in one complex variable that fix 0. Every time we apply P, 0 remains fixed, but what happens to points near 0? For instance, if z is close to 0, is P(P(z)) close to 0? In complex dynamics, this type of question is of great interest.
We will discuss some of the interesting things that can happen in one complex variable. This talk will build up to the famous Leau-Fatou Flower Theorem, which provides a beautiful description of the movement of points near the fixed point for a special type of polynomial. This theorem from the early 1900s serves as inspiration for research in higher dimensions.
- Abstract:
-
Ms. Leyda Almodovar (University of Iowa): "Applications of Persistent Homology"
Monday, February 15, 2016 at 11:00 a.m. in Lytle Hall 228
- Abstract:
Topological Data Analysis (TDA) is a relatively new area within data analysis that combines different disciplines, such as computational topology, statistics and geometry. Many different fields have benefited from this new way of visualizing and analyzing data, such as neuroscience, linguistics and chemistry, and it is especially helpful when applied to network data.
Networks, a set of vertices representing real-world objects and a set of edges denoting relations between vertices, are very useful to model certain relations between groups of objects. In particular, I am interested in the case where these objects are brain regions, and their relations are given by anatomical connections. While the theory points to a lack of connections in certain brain regions in schizophrenic patients, neuroscientists have not been able to identify these regions using standard network theory tools.
I will present the application of persistent homology, the cornerstone of TDA, to different data sets including linguistic data, evasion paths in mobile sensor networks, and brain networks, which will be emphasized.
- Abstract:
-
Dr. Sabrina H. Streipert (Missouri University of Science and Technology): "The Optimal Harvesting Policy for the Beverton-Holt Population Model"
Thursday, February 11, 2016 at 3:00 p.m. in Lytle Hall 228
- Abstract:
In this presentation, the exploitation of a single population modeled by the Beverton-Holt difference equation with periodic coefficients is established. The investigation begins with the harvesting of a single autonomous population with logistic growth and it is shown that the harvested logistic equation with periodic coefficients has a unique positive periodic solution which globally attracts all its solutions. Further, the optimal harvesting policy that maximizes the annual sustainable yield is investigated in a novel and powerful way; it serves as a foundation for the analysis of the exploitation of the discrete population model.
In the second part, the harvested Beverton - Holt model is presented and the unique periodic solution, which globally attracts all its solutions, is derived. The investigation continues by optimizing the sustainable yield with respect to the harvest effort. The results differ from the optimal harvesting policy for the continuous logistic model, which suggests a separate strategy for populations modeled by the Beverton-Holt difference equation.
- Abstract:
-
Dr. Karen Keene (North Carolina State University): "Hands-on Dynamical Systems"
Monday, February 15, 2016 at 11:00 a.m. in Lytle Hall 228
- Abstract:
In her talk, Dr. Keene will offer a hands on way for students to be introduced to the notion of solutions for dynamical systems. Participants in the colloquium will use pipe cleaners to construct an understanding of what a solution to a dynamical system looks like. Then specialized technology will move students into a more formal understanding.
Come prepared to listen, talk and work in a fun area of mathematics.
- Abstract:
-
Dr. Jesse Feller (Kutztown University): "Classical and Generalized Iteration"
Tuesday, November 3, 2015 at 4:00 p.m. in Lytle Hall 228
- Abstract:
The study of holomorphic dynamical systems (discrete time) is a relatively new area of study involving the repeated composition of a single function f(z) in a process called iteration. Thus we are studying the convergence of the sequence of functions fn(z) = (f ◦ f ◦ ... ◦ f)(z) (n times). We will discover the concept of periodic points and classify them into the three categories of attracting, repelling or neutral. Most of our examples have dynamical properties that are easily understood. Other examples have dynamical properties that are called chaotic due to their unpredictability. We will take a look at several computer generated images of the important Julia and filled Julia sets for several examples.
Some mathematicians studying dynamics focus on composing a different function at each step of the iteration process where the function is chosen from a family according to some probability distribution. This is called random iteration. We will learn about a few recent results in this area regarding the probability that a random iteration ends up “close” to an attracting periodic point.
- Abstract:
-
Dr. James Hammer (Cedar Crest College): "Factor Pair Latin Squares: Be There or Be Square"
Wednesday, October 14, 2015 at 4:00 p.m. in Lytle Hall 228
- Abstract:
Sudoku has risen in popularity over the past few years. The rules are simple, yet the solutions are often less than trivial. Mathematically, these puzzles are interesting in their own right. This talk will use the idea of a Sudoku puzzle to define a new kind of n x n array. Further, we will aim to prove some necessary (and on occasion sufficient) conditions for the existence of these arrays. To that end, we define a Latin square of order n as an n x n array where every row and every column contain every symbol 1,2,...,n exactly once. We say (a,b) is an ordered factor pair of the integer n if n = a x b. An (a,b)-Sudoku Latin square is a Latin square where in addition to each row and column containing every symbol exactly once, each a x b rectangle also contains every symbol exactly once when the n x n array is tiled with a x b rectangles in the natural way. A factor pair Latin square of order n (denoted FPLS(n)) is an (a,b)-Sudoku Latin square for every factor pair (a,b) of n. This talk will mainly be concerned with the existence of such designs as well as related problems to such designs.
- Abstract:
-
Dr. Craig Bauer (York College): "Unsolved! History's Greatest Ciphers"
Tuesday, September 15, 2015 at 4:00 p.m. in Boehm Hall 261
-
Dr. Patrick Rault (State University of New York at Geneseo): "Numerical ranges: from matrices to pretty pictures"
Thursday, September 10, 2015 at 4:00 p.m. in Lytle Hall 228
2014-2015
-
Dr. Gil Clary, Dr. Gail Craig and Dr. Robert Ziegenfus: "Learning Communities: Theory, Models, Applications, etc."
Thursday, January 29, 2015 at 3:00 p.m. in Lytle Hall 218
-
Dr. Tom Pirnot (Prof. Emeritus of Mathematics, KU): "Glitzy Math: The Mathematics of Computer Graphics"
Thursday, December 4, 2014 at 3:00 p.m. in Boehm Hall 260
-
Brian Kronenthal, Ph.D. (Assistant Prof. of Mathematics, KU): "Fun with Factoring Fantastic Forms"
Thursday, October 2, 2014 at 3:00 p.m. in Lytle Hall 228
2013-2014
-
W. H. Tony Wong, Ph.D. (Assistant Prof. of Mathematics, KU): "Catalan Numbers"
Thursday, April 17, 2014 at 3:00 p.m. in Lytle Hall 214
-
Mr. Zachary Bales and Ms. Lauren Williams (Kutztown University '14): "Those Summer Math Nights"
Thursday, November 21, 2013 at 11:00 a.m. in Lytle Hall 228
-
Joshua Goodson, Ph.D. (Assistant Prof. of Mathematics, KU): "Beliefs of Mathematics Majors"
Thursday, October 17, 2013 at 11:00 a.m. in Lytle Hall 228
2012-2013
-
Jianqiang Zhao (Associate Prof. of Mathematics, Eckerd College): "Hopf Algebra Structure of Generalized Scissors Congruence Groups"
Thursday, February 28, 2013 at 3:00 p.m. in Lytle Hall 214
-
Baldvin Einarsson (University of California at Santa Barbara): "Individual Based and Dynamic Energy Budget Models"
Tuesday, February 19, 2013 at 3:00 p.m. in Lytle Hall 214
-
D.P. Roberts (Assistant Prof. of Mathematics, Illinois Wesleyan University): "Decomposing Graphs into Stars and Hyperstars "
Friday, February 15, 2013 at 3:00 p.m. in Lytle Hall 214
-
S.E. Law (North Carolina State University): "The Hopf Algebra of Sashes "
Tuesday, February 12, 2013 at 3:00 p.m. in Lytle Hall 214
-
B.G. Kronenthal (University of Delaware): "Spying on Cages, Generalized Quadrangles and Moore!"
Tuesday, February 5, 2013 at 3:00 p.m. in Lytle Hall 214
-
Dr. Eric Landquist (Assistant Prof. of Mathematics, KU): "Blood, Sweat and Tears: the Cable-Trench Problem and some Applications"
Thursday, November 1 2012 at 11:00 a.m. in Lytle Hall 228
-
Dr. Jennifer Franko Vasquez (Assistant Prof. of Mathematics, University of Scranton): "Braids, Permutations and Games"
Thursday, October 18, 2012 at 3:30 p.m. in Lytle Hall 228
2011-2012
-
Mr. Patrick Wiltrout (Kutztown University '11): "On the Collatz Conjecture," a MILK Lecture
Thursday, March 8, 2012 at 11:00 a.m. in Lytle Hall 228
-
Mr. John Paul Jablonski (Kutztown University '13): "On Cardinality of Sets: What does `Big' or `Small' Really Mean?," a MILK Lecture
Thursday, March 1, 2012 at 11:00 a.m. in Lytle Hall 228
-
Mr. Clinton Watton (Kutztown University '13): "Research Experience for Undergraduates- Research Report," a MILK Lecture
Thursday, February 23, 2012 at 11:00 a.m. in Lytle Hall 228
-
Dr. Craig Culbert (Assistant Prof. of Mathematics, KU): "From Finite Geometries to Translation Planes"
Thursday, February 16, 2012 at 11:00 a.m. in Lytle Hall 228
-
Dr. Padraig McLoughlin (Associate Prof. of Mathematics, KU): "Aspects of Some Interesting Sets: A Primer"
Thursday, November 17, 2011 at 11:00 a.m. in Lytle Hall 228
-
Dr. Alex Meadows (Assistant Prof. of Mathematics, St. Mary's College of Maryland): "Thoughts on a Modified Moore Method Course in Undergraduate Analysis," a MILK Lecture
Tuesday, November 8, 2011 at 5:00 p.m. in Boehm Hall 260
-
Dr. Alex Meadows (Assistant Prof. of Mathematics, St. Mary's College of Maryland): "Chomp, Chomp, Bechewy Chomp: Math and Games
Tuesday, November 8, 2011 at 11:00 a.m. in Lytle Hall 228
-
Ms. Ashley Dougherty (KU '12): "Research Experience for Undergraduates- Research Report," a MILK Lecture
Thursday, October 20, 2011 at 11:00 a.m. in Lytle Hall 228
-
Dr. Ryan Gantner (Assistant Prof. of Mathematics, St. John Fisher College): "Using Math to Make Games fun"
Thursday, October 6, 2011 at 11:00 a.m. in Lytle Hall 228
Archives of previous colloquia are available here.
Mathematics Inquiry Learning at Kutztown (MILK) Lectures are funded by the generous support of the Academy for Inquiry-Based Learning, The Educational Advancement Foundation, and Mr. Harry Lucas, Jr.